想象这样一个场景：

你正在参加一个游戏节目。主持人指着面前的三扇门，告诉你：其中一扇门后面是一辆全新汽车，另外两扇门后面各藏着一只羊。你需要选择一扇门。

假设你选择了1号门。这时，主持人（他知道每扇门后面是什么）打开了2号门，露出了一只羊。现在他给你一个机会：你要坚持自己的选择，还是换成剩下的3号门？

大多数人会选择坚持原来的选择，这往往源于纯粹的心理因素。而那些试图用逻辑思考的人则会得出"换不换都一样"的结论。

毕竟现在只剩下两扇门了，似乎我们并不知道哪扇门后面有汽车...但，真的是这样吗？

事实上，最优策略是换门！而且换门会让你的获胜概率直接翻倍！

这就是著名的蒙提霍尔悖论。

虽然这个问题已经被数学证明，答案也被广泛接受，但它仍然是一个常常引起争议、让人困惑的话题。

普通的解释往往只会让质疑者更加困惑。

所以在这篇文章中，我将深入探讨其中的原因，这可以看作是一个"解释的解释"。

历史背景

这个问题的名字来源于美国60年代一个叫《让我们做个交易》的游戏节目主持人蒙提·霍尔。

在原版节目中，游戏规则并不像现在这个数学问题那么严格。有时候主持人会提供现金让选手放弃换门的机会，有时候他的行为也会受到电视效果的影响。

1990年，专栏作家玛丽莲·沃斯·萨凡特在她的"问玛丽莲"专栏中，将这个场景简化成了一个数学问题：主持人总是会显示一只羊，并且总是会给出换门的机会。

结论是：换门能将获胜概率从1/3提升到2/3。

这个结论立即引发了轩然大波。许多教授、数学家和怀疑论者纷纷写信指责她的错误。即便在看到详细的数学证明后，依然有人拒绝接受这个结论。

叙事与数学的对决

从本质上来说，蒙提霍尔问题是直觉和抽象思维的较量。

当我们遇到这种情况时，我们的思维很自然地会被拉向叙事的方向——关注情景中的人性化因素，比如"主持人是不是在耍我"之类的问题。

这些都是很自然的疑问，但它们实际上混淆了问题的本质。

数学模型并不关心主持人的动机或者你的信任问题。它们是抽象的，是经过简化的模型，目的是揭示潜在的概率关系。它们剥离了人类行为的复杂性，给出明确的答案。

在现实世界中，我们可能需要考虑这些心理因素。

但在这个悖论中，唯一找到答案的方法就是相信抽象模型。

要理解这个解决方案，我们必须理解游戏的严格规则，并且同意解决抽象问题就等于解决了原始问题。以下是规则：

1. 有三扇门，一扇后面是汽车，两扇后面是羊
2. 你选择一扇门
3. 主持人必须打开一扇不同的门来展示一只羊
4. 你可以选择换到剩下的那扇门

重要的是，在这个版本中，主持人可以被视为一个机器人。

（我们可以添加规则3.1：如果主持人可以在你没选的门中打开任意一扇展示羊，他总是选择号码更小的那扇门或抛硬币决定。这种机械的选择不会改变获胜的概率。）

在文章开头的版本中，规则3并没有被明确说明。

然而，主持人知道汽车的位置并且被迫打开一扇有羊的门（而且不是你选的那扇）这个事实是整个问题的关键！

所以，要理解为什么换门更好，你必须接受这些就是游戏规则。

100扇门，99只羊

让我们看看玛丽莲·沃斯·萨凡特最喜欢的解释方式——"100扇门，99只羊"版本。

这个解释通过放大问题规模来使逻辑更直观。夸张的场景有助于突出为什么换门是更好的选择。

来看看：

假设现在有100扇门，你知道其中一扇后面是一辆新车，其他99扇后面都是羊。主持人让你选择一扇门。你选择了1号门。

接下来，主持人开始打开门，每打开一扇门都露出一只羊。他从2号门开始，一直开到100号门。有趣的是，他跳过了29号门没开。

现在他给你一个机会：换到29号门，或者坚持你最初的选择。你会怎么选？

大多数人都承认，在99扇门中特意跳过一扇不开，这个行为足以说服他们换到那扇门。

但是这个解释也有一个问题。

它需要抽象思维能力，需要能够将一个场景的洞见转移到另一个场景。虽然放大问题规模突出了换门的压倒性优势，但它要求听众能够认识到100扇门场景的逻辑同样适用于3扇门的版本。

这对很多人来说并不直观。

许多人会关注具体的数字或者100扇门的特殊设置，而不是理解概率重分配的核心原理。

如果不能在夸张的例子和原始问题之间架起桥梁，这个"100扇门，99只羊"的解释对那些难以泛化抽象概念的人来说可能感觉脱节且无说服力。

穷举分析

另一个常见的解释方法是详细列出所有可能的情况——这种方法叫做穷举搜索。通过展示每种可能的组合及其结果，这种方法让答案变得无可争议。

通过详细的列表，一个清晰的模式就会显现出来：

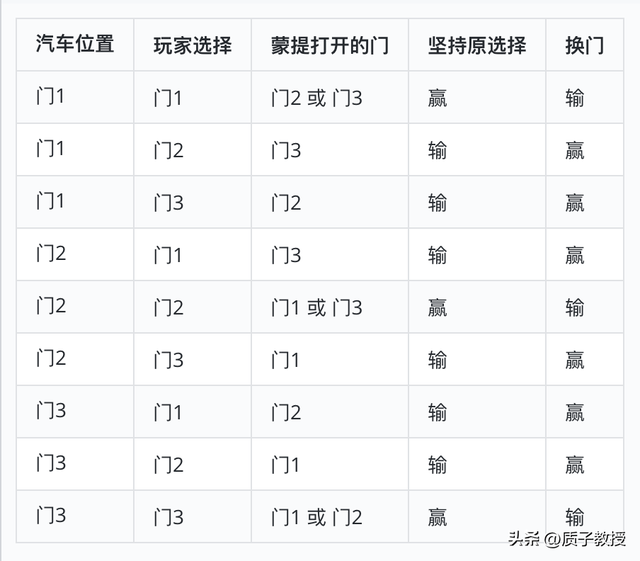
• 在1/3的情况下，坚持原选择会赢（当你的初始选择恰好正确时）
• 在2/3的情况下，换门会赢（当汽车在你最初没选的两扇门之后时）

这个解释非常具体。然而，即便是这种解释方法也有其局限性。

穷举搜索需要检查每一种可能的情况。虽然逻辑严密，但案例数量可能令人感到繁琐，有些人可能会忽视其中的规律。

即使看到了这些，许多人仍然坚持认为在主持人显示一只羊后，剩下两扇门的概率应该是50:50。穷举搜索可以显示这是错误的，但它并不能解释为什么——这让一些怀疑者仍然无法信服。

模拟实验：最直观的证明

如果思考99只羊或者穷举分析让你感到乏味，那么还有另一种解决蒙提霍尔问题的方法：运行模拟实验。

这种方法不需要高深的数学知识——只需要让计算机模拟数千次游戏，然后统计换门和不换门的获胜次数。

就连著名数学家保罗·埃尔德什，以其对直觉论证的怀疑而闻名，据说也是在看到模拟结果后才被说服的。而且你不需要成为数学家就能运行这样的实验。

通过简单的在线搜索，任何人都能找到工具在几分钟内模拟上千次蒙提霍尔问题。

在一次2000次的模拟中，结果显示：

坚持原选择：赢得概率约33%

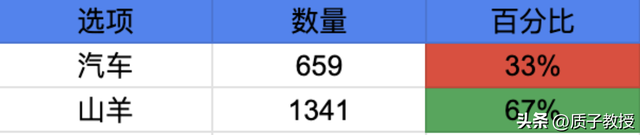
选择换门：赢得概率约67%

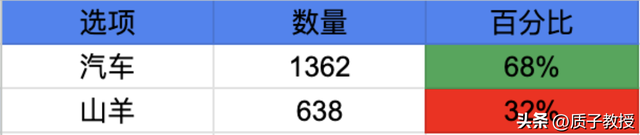
这个结果完美印证了理论预测的1/3和2/3概率。

模拟实验是一种直接、务实的方式来证明换门的优势。它超越直觉，专注于冷酷的结果数据。这是经验科学的胜利！

然而，即便是模拟实验也有其批评者。

模拟可以告诉你换门更好，但它不能告诉你为什么。对于那些寻求更深层理解的人来说，单纯的数字可能让你感觉不够满意。

你的选择与其他选项

另一种解释蒙提霍尔悖论的方法是将问题重新框定为"你的初始选择"与"其他所有选择"之间的对比。这种方法关注的是换门实际上给了你所有未选门的优势。它简化了概率，突出了为什么换门是更好的策略。

在你做出选择后，主持人打开了另外两扇门中的一扇来展示一只羊。这个行为并不改变你初始选择的概率：

• 你选择的门后面有车的概率仍然是1/3
• 车在另外两扇门后面的2/3概率并没有消失。相反，主持人的行为将这个概率集中到了剩下的那扇未开启的门上

如果你在游戏开始前就决定要换门，这就相当于在说："我不相信我的初始1/3概率选择。

相反，我要赌车在另外两扇门中的某一扇后面。"由于主持人总是会从那对门中显示一只羊，你的换门策略保证了你能"继承"这两扇门的组合概率2/3在他的展示之后。

这就是为什么换门更好。因为这不仅仅是关于选择单个门，而是关于利用主持人的展示来获得两扇未选门的组合概率。

然而，这种方法可能会让怀疑者觉得游戏被操纵或抽象成了别的东西。

人们直觉上会将门视为独立的个体，而不是群组。

换门能让你获得"两扇"未选门的好处这个想法感觉像是一个把戏——毕竟，主持人只留下了一扇未开启的门，它怎么能代表两扇门的机会呢？

贝叶斯推理

在统计学家中最受欢迎的解释是贝叶斯方法。它不会遗漏任何细节。

然而，你需要知道——或者至少相信——基于新信息更新概率必须使用贝叶斯定理。

对于任意两个陈述"A"和"B"，贝叶斯定理可以表示为：

P(A|B) = P(B|A) × P(A) / P(B)

等式左边表示：在已知B的条件下A的概率。B通常是我们已知为真或刚刚发现为真的事情。为了便于讨论，让我们假设我们选择了1号门，刚刚发现主持人打开了3号门显示了一只羊。

所以，我们想知道在主持人打开3号门的条件下，2号门后面有车的概率。要计算这个，我们需要使用贝叶斯定理。为此，我们需要知道等式右边的三个概率。

首先，计算过程如下：

P(车在2号门|主持人开3号门) =

P(主持人开3号门|车在2号门) × P(车在2号门) / P(主持人开3号门)

= 1 × (1/3) / (1/2)

= 2/3

我们是如何得到这个结果的？让我们逐步分析：

1. 如果车在2号门后面，主持人打开3号门的概率是1。在这种情况下，主持人别无选择。
2. 车在2号门后面的无条件概率——所谓的先验概率——是1/3。这是最初猜中正确门的概率。
3. 最后一个概率是主持人打开3号门的概率，但是(!)不考虑车的位置信息。如果我们假设主持人不知道车在哪里，他打开2号门或3号门的概率各是1/2。

就是这样！将这些数字代入贝叶斯定理揭示了我们没选的那扇门后面有车的概率是2/3。也就是说，我们应该换门！

现在，你可能会认为同样的计算也适用于车在1号门（你最初的选择）后面的情况。但是不是！后两个概率是相同的，但第一个不是。

P(车在1号门|主持人开3号门) =

P(主持人开3号门|车在1号门) × P(车在1号门) / P(主持人开3号门)

= (1/2) × (1/3) / (1/2)

= 1/3

当车在1号门（你的初始选择）后面时，主持人打开3号门的概率不是1。在这种情况下，主持人确实有选择——他可以打开2号门或3号门。

因此，这个概率是1/2，计算结果显示你最初选择的门后面有车的概率仍然是1/3。

当然，要理解所有这些，你需要按自己的节奏仔细思考，可能还需要自己重新从头计算一遍。但是如果你这样做了，你一定能理解。

为什么有些人永远不会理解

问题不在于数学，而在于我们的思维方式。

蒙提霍尔悖论迫使我们要推翻关于公平性、随机性和概率的根深蒂固的直觉。大多数人本能地认为在主持人揭示后所有选项必须是同样可能的，因为这感觉更公平。

信息（主持人的揭示）能改变概率而不改变物理设置这个想法是极其反直觉的。

对于那些信任抽象思维并坚持数学逻辑的人来说，答案是明确的：换门会赢。对于那些无法或选择不从叙事中脱离的人来说，任何解释都永远不够。

但这不仅仅是一个游戏。蒙提霍尔悖论是我们处理生活问题方式的缩影。当面对复杂情况时，我们的本能往往会误导我们。

抽象、简化和数学推理是帮助我们穿透噪音的工具，即使它们与我们的直觉相冲突。